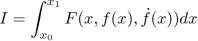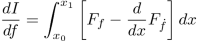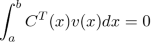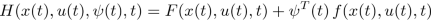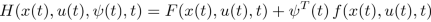Dynamic Optimization

Dynamic optimization deals with problems where the solution depends on time or space. It is exposed under different angles. First, from a purely mathematical point of view, the problem is solved based on variational calculus. First order Euler conditions are demonstrated, and second order Legendre–Clebsch are mentioned. The same problem is discussed using Hamilton–Jacobi framework. Then, dynamic optimization in continuous time is treated in the framework of optimal control. Successively, Euler’s method, Hamilton–Jacobi, and Pontryagin’s maximum principle are exposed. Several detailed examples accompany the different techniques. Numerical issues with different solutions are explained. The continuous-time part is followed by the discrete-time part, i.e. dynamic programming. Bellman’s theory is explained both by backward and forward induction with clear numerical examples.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save
Springer+ Basic
€32.70 /Month
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Buy Now
Price includes VAT (France)
eBook EUR 58.84 Price includes VAT (France)
Softcover Book EUR 73.84 Price includes VAT (France)
Hardcover Book EUR 105.49 Price includes VAT (France)
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
A functional is a function of functions; the function depends on functions and .
- (a) We denote by yz the partial derivative ∂y∕∂z, where z is a scalar. If y is scalar and a vector, the notation is the gradient vector of partial derivatives ∂y∕∂zi. If and are vectors, the notation represents the Jacobian matrix of typical element ∂yi∕∂zj.
- (b) The derivative with respect to of the integral with fixed boundaries
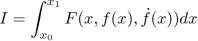
is equal to
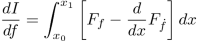
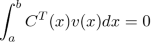
Other authors use the definition of the Hamiltonian with an opposite sign before the functional, that is,
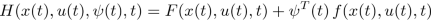
which changes nothing, as long as we remain at the level of first-order conditions. However, the sign changes in condition (12.4.21). See also the footnote in Section 12.4.6.
In many articles, authors refer to the Minimum Principle, which simply results from the definition of the Hamiltonian H with an opposite sign of the functional. Comparing to definition (12.4.36), they define their Hamiltonian as
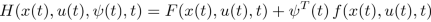
With that definition, the optimal control u ∗ minimizes the Hamiltonian.
This notation is that of Pontryaguine et al. (1974). The superscript corresponds to the rank i of the coordinate, while the subscripts (0 and 1) or (0 and f), according to the authors, are reserved for the terminal conditions.
References
- R. Aris. Studies in optimization. II. Optimal temperature gradients in tubular reactors. Chem. Eng. Sci., 13 (1): 18–29, 1960. Google Scholar
- R. Aris. The Optimal Design of Chemical Reactors: a Study in Dynamic Programming. Academic Press, New York, 1961. MATHGoogle Scholar
- R. Aris, D. F. Rudd, and N. R. Amundson. On optimum cross current extraction. Chem. Eng. Sci., 12: 88–97, 1960. ArticleGoogle Scholar
- J. R. Banga and E. F. Carrasco. Rebuttal to the comments of Rein Luus on ”Dynamic optimization of batch reactors using adaptive stochastic algorithms”. Ind. Eng. Chem. res., 37: 306–307, 1998. ArticleGoogle Scholar
- R. J. Barro and X. Sala-I-Martin. Economic Growth. McGraw-Hill, New York, 2004. MATHGoogle Scholar
- R. Bellman. Dynamic Programming. Princeton University Press, Princeton, New Jersey, 1957. MATHGoogle Scholar
- R. Bellman and S. Dreyfus. Applied Dynamic Programming. Princeton University Press, Princeton, New Jersey, 1962. BookMATHGoogle Scholar
- D. P. Bertsekas. Dynamic Optimization and Optimal Control. Athena Scientific, Belmont, 2017. Google Scholar
- L. T. Biegler. Solution of dynamic optimization problems by successive quadratic programming and orthogonal collocation. Comp. Chem. Eng., 8: 243–248, 1984. ArticleGoogle Scholar
- M. Blanco Fonseca and G. Flichman. Bio-Economic Models applied to Agricultural Systems, chapter Dynamic Optimisation Problems: Different Resolution Methods Regarding Agriculture and Natural Resource Economics, pages 29–57. Springer-Verlag, 2011. Google Scholar
- B. Bojkov and R. Luus. Optimal control of nonlinear systems with unspecified final times. Chem. Eng. Sci., 51 (6): 905–919, 1996. ArticleGoogle Scholar
- P. Borne, G. Dauphin-Tanguy, J. P. Richard, F. Rotella, and I. Zambettakis. Commande et optimisation des processus. Technip, Paris, 1990. MATHGoogle Scholar
- R. Boudarel, J. Delmas, and P. Guichet. Commande optimale des processus. Dunod, Paris, 1969. MATHGoogle Scholar
- A. E. Bryson. Dynamic Optimization. Addison Wesley, Menlo Park, California, 1999. Google Scholar
- A. E. Bryson and Y. C. Ho. Applied Optimal Control. Hemisphere, Washington, 1975. Google Scholar
- A. Calogero. Notes on optimal control theory with economic models and exercises. Technical report, Università di Milano-Bicocca, 2020. Google Scholar
- J. Cao and G. Illing. Instructor’s Manual for Money: Theory and Practice. Springer Nature Switzerland, 2019. Google Scholar
- E. F. Carrasco and J. R. Banga. Dynamic optimization of batch reactors using adaptive stochastic algorithms. Ind. Eng. Chem. Res., 36: 2252–2261, 1997. ArticleGoogle Scholar
- H. Cartan. Cours de calcul différentiel. Hermann, Paris, 1967. MATHGoogle Scholar
- W. C. Chan. An Elementary Introduction to Queueing Systems. World Scientific, 2014. BookMATHGoogle Scholar
- A. C. Chiang. Elements of Dynamic Optimization. Waveland Press, Long Grove, IL, 1992. Google Scholar
- J. P. Corriou. Process control - Theory and applications. Springer, London, 2nd edition, 2018. BookGoogle Scholar
- J. P. Corriou and S. Rohani. A new look at optimal control of a batch crystallizer. AIChE J., 54 (12): 3188–3206, 2008. ArticleGoogle Scholar
- L. Cretegny and T. F. Rutherford. Worked examples in dynamic optimization: analytic and numeric methods. Technical report, Centre of Policy Studies, Monash University, Australia, 2004. Google Scholar
- J. E. Cuthrell and L. T. Biegler. On the optimization of differential-algebraic process systems. A.I.Ch.E. J., 33: 1257–1270, 1987. ArticleMathSciNetGoogle Scholar
- J. N. Farber and R. L. Laurence. The minimum time problem in batch radical polymerization: a comparison of two policies. Chem. Eng. Commun., 46: 347–364, 1986. ArticleGoogle Scholar
- A. Feldbaum. Principes théoriques des systèmes asservis optimaux. Mir, Moscou, 1973. Edition Française. Google Scholar
- M. Fikar, M. A. Latifi, J. P. Corriou, and Y. Creff. CVP-based optimal control of an industrial depropanizer column. Comp. Chem. Engn., 24: 909–915, 2000. ArticleGoogle Scholar
- R. Fletcher. Practical Methods of Optimization. Wiley, Chichester, 1991. MATHGoogle Scholar
- H. S. Fogler. Elements of Chemical Reaction Engineering. Prentice-Hall, Boston, 5th edition, 2016. Google Scholar
- C. Gentric, F. Pla, M. A. Latifi, and J. P. Corriou. Optimization and non-linear control of a batch emulsion polymerization reactor. Chem. Eng. J., 75: 31–46, 1999. ArticleGoogle Scholar
- C. J. Goh and K. L. Teo. Control parametrization: a unified approach to optimal control problems with general constraints. Automatica, 24: 3–18, 1988. ArticleMathSciNetMATHGoogle Scholar
- G. Gutin and A. P. Punnen, editors. The Traveling Salesman Problem and Its Variations. Springer, New York, 2007. MATHGoogle Scholar
- P. Hagelauer and F. Mora-Camino. A soft dynamic programming 4D-trajectory approach for on-line aircraft optimization. European Journal of operational Research, 107: 87–95, 1998. ArticleMATHGoogle Scholar
- R. C. Hampshire and W. A. Massey. Dynamic optimization with applications to dynamic rate queues. Tutorials in Operations Research, pages 208–247, 2010. Google Scholar
- C. Hansknecht, I. Joormann, and S. Stiller. Dynamic shortest paths methods for the time-dependent TSP. Algorithms, 14, 2021. Google Scholar
- A Harada and Y. Miyazawa. Dynamic programming applications to flight trajectory optimization. In 19th IFAC Symposium on Automatic Control in Aerospace, Würzburg, Germany, pages 441–446, 2013. Google Scholar
- R. H. W. Hoppe. Optimization theory. Technical report, University of Houston, 2007. Google Scholar
- H. Hotelling. The economics of exhaustible resources. Journal of Political Economy, 39: 137–175, 1931. ArticleMATHGoogle Scholar
- S. W. Hur, S. H. Lee, Y. H. Nam, and C. J. Kim. Direct dynamic-simulation approach to trajectory optimization. Chinese Journal of Aeronautics, 2021. Google Scholar
- M. L. Kamien and N. L. Schwartz. Dynamic Optimization - The calculus of variations and optimal control in Economics and Management. North-Holland, Amsterdam, 2nd edition, 1991. MATHGoogle Scholar
- A. Kaufmann and R. Cruon. La programmation dynamique. Gestion Scientifique Séquentielle. Dunod, Paris, 1965. Google Scholar
- J. O. S. Kennedy. Principles of dynamic optimization in resource management. Agricultural Economics, 2: 57–72, 1988. ArticleGoogle Scholar
- D. E. Kirk. Optimal control theory. An introduction. Prentice-Hall, Englewood Cliffs, New Jersey, 1970. Google Scholar
- L. Kleinrock. Queueing Systems. Volume I: Theory. Wiley, New York, 1975. Google Scholar
- Y. D. Kwon and L. B. Evans. A coordinate transformation method for the numerical solution of non-linear minimum-time control problems. AIChE J., 21: 1158–, 1975. Google Scholar
- F. Lamnabhi-Lagarrigue. Singular optimal control problems: on the order of a singular arc. Systems & control letters, 9: 173–182, 1987. ArticleMathSciNetMATHGoogle Scholar
- M. A. Latifi, J. P. Corriou, and M. Fikar. Dynamic optimization of chemical processes. Trends in Chem. Eng., 4: 189–201, 1998. Google Scholar
- E. B. Lee and L. Markus. Foundations of Optimal Control Theory. Krieger, Malabar, Florida, 1967. MATHGoogle Scholar
- O. Levenspiel. Chemical Reaction Engineering. Wiley, New York, 3rd edition, 1999. Google Scholar
- R. Luus. Application of dynamic programming to high-dimensional nonlinear optimal control systems. Int. J. Cont., 52 (1): 239–250, 1990. ArticleMathSciNetMATHGoogle Scholar
- R. Luus. Application of iterative dynamic programming to very high-dimensional systems. Hung. J. Ind. Chem., 21: 243–250, 1993. Google Scholar
- R. Luus. Optimal control of bath reactors by iterative dynamic programming. J. Proc. Cont., 4 (4): 218–226, 1994. ArticleGoogle Scholar
- R. Luus. Numerical convergence properties of iterative dynamic programming when applied to high dimensional systems. Trans. IChemE, part A, 74: 55–62, 1996. Google Scholar
- R. Luus and B. Bojkov. Application of iterative dynamic programming to time-optimal control. Chem. Eng. Res. Des., 72: 72–80, 1994. Google Scholar
- R. Luus and D. Hennessy. Optimization of fed-batch reactors by the Luus-Jaakola optimization procedure. Ind. Eng. Chem. Res., 38: 1948–1955, 1999. Google Scholar
- W. Mekarapiruk and R. Luus. Optimal control of inequality state constrained systems. Ind. Eng. Chem. Res., 36: 1686–1694, 1997. Google Scholar
- S. Minner. Multiple-supplier inventory models in supply chain management: A review. Int. J. Production Economics, 81–82: 265–279, 2003. ArticleGoogle Scholar
- T. Mitra. Optimization and Chaos, chapter Introduction to Dynamic Optimization Theory. Springer-Verlag, Heidelberg, 2000. Google Scholar
- A. Perea. Backward induction versus forward induction reasoning. Games, 1: 168–188, 2010. ArticleMathSciNetMATHGoogle Scholar
- A. Perea. Epistemic Game Theory: Reasoning and Choice. Cambridge University Press, Cambridge, 2012. BookGoogle Scholar
- L. Pontryaguine, V. Boltianski, R. Gamkrelidze, and E. Michtchenko. Théorie mathématique des processus optimaux. Mir, Moscou, 1974. Edition Française. Google Scholar
- L. Pun. Introduction à la pratique de l’optimisation. Dunod, Paris, 1972. MATHGoogle Scholar
- M. L. Puterman. Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley, Chichester, 1994. BookMATHGoogle Scholar
- E. P. Ramsey. A mathematical theory of saving. Economic Journal, 38: 543–559, 1928. ArticleGoogle Scholar
- W. H. Ray and J. Szekely. Process Optimization with applications in metallurgy and chemical engineering. John Wiley, New York, 1973. Google Scholar
- S. M. Roberts. Dynamic Programming in Chemical Engineering and Process Control. Academic Press, New York, 1964. Google Scholar
- S. M. Roberts and C. G. Laspe. Computer control of a thermal cracking reaction. Ind. Eng. Chem., 53 (5): 343–348, 1961. ArticleGoogle Scholar
- K. Schittkowski. NLPQL: a Fortran subroutine solving constrained nonlinear programming problems. Annals of Operations Research, 5: 485–500, 1985. ArticleMathSciNetGoogle Scholar
- L. I. Sennott. Stochastic Dynamic Programming and the Control of Queueing Systems. Wiley, New York, 1999. MATHGoogle Scholar
- S. P. Sethi and G. Thompson. Optimal Control Theory: Applications to Management Science and Economics. Springer-Verlag, 2000. MATHGoogle Scholar
- R. Soeterboek. Predictive Control - A Unified Approach. Prentice Hall, Englewood Cliffs, New Jersey, 1992. Google Scholar
- R. F. Stengel. Optimal control and estimation. Courier Dover Publications, 1994. MATHGoogle Scholar
- V. Sundarapandian. Probability, Statistics and Queueing Theory. PHI Learning, 2009. Google Scholar
- K. L. Teo, C. J. Goh, and K. H. Wong. A Unified Computational Approach to Optimal Control Problems. Wiley and Sons, Inc., New York, 1991. MATHGoogle Scholar
- T. Todorova. Mathematics for Economists: Problems Book. Wiley-Blackwell, Hoboken, 2011. Google Scholar
- J. A. Vernon and W. K. Hughen. A primer on dynamic optimization and optimal control in pharmacoeconomics. Value in Health, 9 (2): 106–113, 2006. ArticleGoogle Scholar
Author information
Authors and Affiliations
- LRGP-CNRS-ENSIC, University of Lorraine, Nancy, France Jean-Pierre Corriou
- Jean-Pierre Corriou